Expresiones

En este capítulo aprenderas la relación entre los tipos de datos y las operaciones válidas que se pueden realizar con ellos. Los conceptos a revisar son:

• expresiones,
• concatenación,
• operaciones aritméticas,
• operaciones relacionales,
• operaciones lógicas,
• prioridad de operaciones.

Tipos de expresiones

Las expresiones son combinaciones de constantes, variables, símbolos de operación, y paréntesis. Por ejemplo: a + (b + 3) / c.

Cada expresión resulta en un valor que se determina al evaluar las operaciones indicadas usando los valores de las variables y constantes implicadas.

Una expresión consta de operadores y operandos. Según sea el tipo de datos que manipulan, las expresiones se clasifican en:

• Aritméticas
• Relacionales
• Lógicas y
• De concatenación

Operadores y Operandos

Los operadores son elementos que relacionan de forma diferente, los valores de una o mas variables y/o constantes. Es decir, los operadores nos permiten manipular valores y se dividen en cuatro grupos como se muestra en la siguiente Figura:

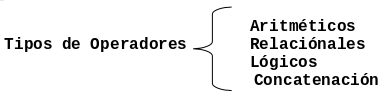
Concatenación

Una operación de concatenación involucra dos o mas valores alafanuméricos o cadenas, cuyo contenido se va agregando al resultado final, evaluando de izquierda a derecha. Generalmente representamos esta operación con el operador +, aunque algunos lenguajes de programación usan un símbolo diferente. Por ejemplo:

"Hola " + "mundo" dará como resultado "Hola mundo"

Operadores Aritméticos

La forma general que tiene una operación aritmética que opera sobre dos valores se ilustra en la siguiente Figura:

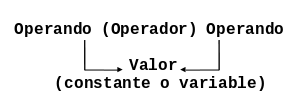
Los operadores aritméticos son válidos para tipos de datos enteros o reales. Si ambos son enteros, el resultado es entero; si alguno de ellos es real, el resultado es real. Las operaciones aritméticas son las siguientes:

• Suma: +
• Resta: -
• Multiplicación: *
• División: /
• Módulo (residuo de la división entera): %
• Exponenciación: ^

Ejemplos:

Prioridad de los Operadores Aritméticos

Las operaciones aritméticas deben evaluarse de acuerdo a la importancia del operador, es decir, de acuerdo a su prioridad, de la siguiente forma:

• Todas las expresiones entre paréntesis se evalúan primero.
• Las expresiones con paréntesis anidados se evalúan de adentro hacia afuera, el paréntesis más interno se evalúa primero.
• Dentro de una misma expresión los operadores se evalúan en el siguiente orden.
  1. Exponenciación: ^
  2. Multiplicación, división, modulo: *, /, %
  3. Suma y resta: +, -
• Los operadores en una misma expresión con igual nivel de prioridad se evalúan de izquierda a derecha.

Ejemplos

4 + 2 * 5 = 14
4 + 10 = 14
23 * 4 / 2 = 46
92 / 2 = 46
3 + 5 * (10 - (2 + 4)) = 23
3 + 5 * (10 - 6) = 3 + 5 * 4 = 3 + 20 = 23
3 + 5 - 14 / 2 = 1
3 + 5 - 7 = 8 - 7 = 1
2 * (1 + 3 * 4) = 26
2 * (1 + 12) = 2 * 13 = 26

Operadores Relacionales

Los operadores relacionales se utilizan para establecer una relación entre dos valores. Los valores se comparan entre sí y esta comparación produce un resultado de certeza o falsedad (verdadero o falso).

Los operadores relacionales deben comparan valores del mismo tipo (numéricos o cadenas), tienen el mismo nivel de prioridad en su evaluación y tienen menor prioridad que los operadores aritméticos.

Las operaciones relacionales son las siguientes:

• > Mayor que
• < Menor que
• >= Mayor o igual que
• <= Menor o igual que
• != Diferente
• == Igual

Ejemplos

Si a = 10, b = 20 y c = 30.

a + b > c

Falso

a - b < c

Verdadero

a - b == c

Falso

a * b != c

Verdadero

Ejemplos no válidos:

a < b < c

10 < 20 < 30

'hola' < 30

Operadores Lógicos

Los operadores lógicos se utilizan para establecer relaciones entre valores lógicos. Estos valores pueden ser resultado de una expresión relacional.

Las operaciones lógicas son las siguientes:

• Conjunción: AND, &
• Disyunción: OR, |
• Negación: NOT, !

A continuación se muestran las tablas de verdad para las operaciones lógicas.

Ejemplos: Sea a = 10, b = 20 y c = 30.

 a < b  & b  < c
10 < 20 & 20 < 30
   V    &    V
       V

Prioridad de los Operadores Lógicos

Los operadores relacionales se evalúan en el siguiente orden.

• Not !
• And &
• OR |

Prioridad de los Operadores en General

A continuación se hace un resumen de la prioridad de los operadores aritméticos, relacionales y lógicos.

1. ()

2. ^

3. *, /, %, !

4. +, -, &

5. >, <, >=, <=, !=, ==, |

Ejemplos:

Sean a = 10, b = 12, c = 13, y d = 10.

((a  > b)  | (a < c))   & ((a == c)   | (a >= b))
((10 > 12) | (10 < 13)) & ((10 == 13) | (10 >= 12))
(    F     |      V   ) & (     F     |     F     ) 
           V            &             F
                        F

((a  >= b)  | (a < d))   & ((a >= d)   & (c  > d ))
((10 >= 12) | (10 < 10)) & ((10 >= 10) & (13 > 10))
(    F      |     F    ) & (    V      &     V    )
            F            &             V
                         F

!(a == c)   & (c  > b)
!(10 == 13) & (13 > 12)
     !F     &     V
     V      &     V
            V

Ejercicios propuestos

1. ¿Que es una expresión y cuál es su clasificación?
2. Realice las siguientes operaciones aritméticas:

   2 + 9 * 3 - 100 / 5
   ((6 * 10 - 45 + 80) / 10) / (((12 + 3) * 5 -45) / 9)
   (((2^10 - 1000) + 76) / (120 - 90 + (25 * 4 / 20))) / 5 + 10
   (20 - 40 + (25 / 5 * 20) / (2 * 10 - 1000 / 50) + 40) / ((6 + 10) / (20 * 10 / 50 * 2))

3. Realice las siguientes operaciones relacionales, con a = 10, b = 5 y c = 20:

   (2 * a / 2 * b) / (a - 5 * a * b + c) > (a + 2 * b + c) - (b + c * 8)
   (2 * a - 5 * b) / (4 * c - 5 * a * b + 10) <= (a * b * c) / (a + b + c)
   (10 * a + 5 + b) / (c - 5 * a * b + 10) != (a + b * c) - (a * b + c) / (5 * a)
   10 / (a + b + c) + 3 * a * b * c == 10 * c - 2 * a * b + 6

4. Realice las siguientes operaciones lógicas, con a = 1, b = 2 y c = 4:

   (2 * a) / (5 * b + 10) > 3 * a + c && 3 * a * b * c >= 200
   a / (5 * b) <= 3 * a + c || a * b * c >= 200 && !(a + b * c >= 350 * c)
   a / (b + c) != 10 * b + a || a + 5 * b * a >= 5 * b / 2 && !(a + b != 2 * c)
   (2 + a) / (5 * b + c) >= 3 + 2 * a && !(5 + 2 * c < 3 * a) && !(3 + a <= 5 * b + c)